はじめに
今までの投稿で、多くのオープンデータを箱ひげ図を使って料理をしてきました。
でもその箱ひげ図とはいったいな何なのか?説明してきてませんでしたね。今回はじっくりと箱ひげ図について説明をする投稿とします。
このような方もいるのではないでしょうか。
- 箱ひげ図って言葉を聞いたことあるけど、いったい何?
- 箱ひげ図ってどうやって見るの?見方を知りたい。
- 「箱」や「ひげ」、変なところにあるプロット(点)は何を意味するの?
- 箱ひげ図のメリットは?デメリットもあるの?
こんな疑問に答えます。
徹底解説!箱ひげ図って何?「箱」や「ひげ」ってどう見る?
箱ひげ図とは、ざっくりと表現するとデータの分布を視覚的に表す方法です。
データのばらつきを可視化して、「箱」と「ひげ」によって構成されたかたまりによって、表現することでデータの分布を俯瞰的に把握することができる図(グラフ)の1つです。
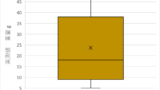
まずは、下記の図を見て下さい。実際の例をみながら説明します。
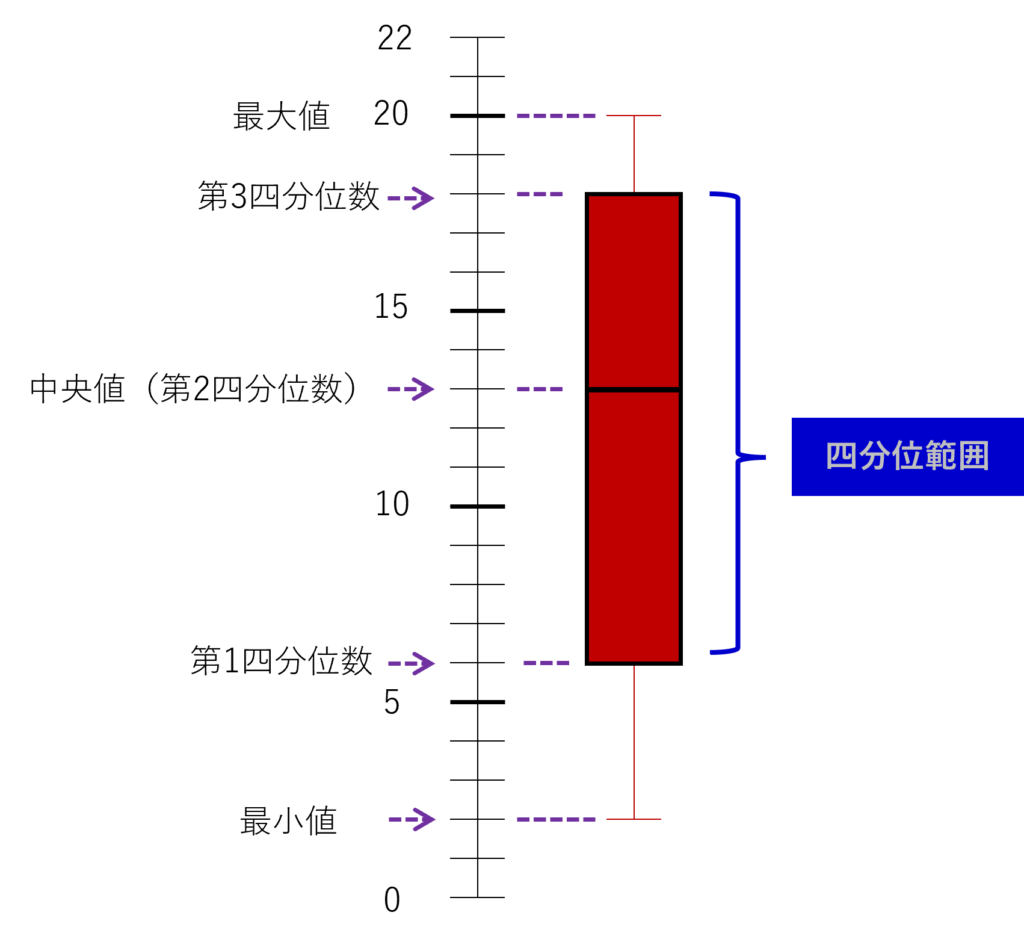
例えば、ある9人がテストして、得られた結果が
7点、5点、19点、11点、20点、16点、13点、2点、17点
であったとします。これを箱ひげ図で視覚化したのが上記の絵となります。確かに上下ともに、両端で線(ひげ)のように伸びており、一方で、真ん中であるほど、棒(箱)があり、つまり「箱」と「ひげ」で構成されているのがわかりますね。これが箱ひげ図です。
ここで、聞き慣れない用語も示されているかと思いますので、1つずつ説明します。
最小値
まさにデータにおける最も小さい値です。今回の場合、9人のテスト点数から2点が最小値(Minimum)となりますね。いわゆる「ひげ」の下端に位置してます。
後述する、「外れ値(Outlier)」も箱ひげ図には考慮する必要があります。上記の絵には出てきてませんが、外れ値がある場合、最小値よりも小さい位置に(さらに下端に)存在するケースがあります。
いずれにせよ、外れ値については後程説明します。
最大値
データにおける最も大きい値です。 今回の場合、9人のテスト点数から20点が最大値(Maximum)となりますね。いわゆる「ひげ」の上端に位置してます。
(※ 同様に、外れ値がある場合は、どのように考えるかは後述します。)
四分位数とは(第1、第2、第3四分位数)
ステップ毎に説明して、四分位数を解説します。先ほどの9人のテスト結果を引き続き、例として使いましょう。
小さい順に並べる(ステップ1)
まず、今回の例の9人のテストの点数をを詳しくみてみるため、小さい順に並べます。ここで、データを小さい方から均等に4分割したものを、四分位数と言います。

中央値(第2四分位数)を求める(ステップ2)
9個並べたデータから中央値を求めます。例では9個しかないので、真ん中(中央)は5番目の13であることは容易にわかりますね。この13が、データが9個の場合の中央値(Median)です。第2四分位数とも呼びます。最小値は2、最大値は20であることも明記します。
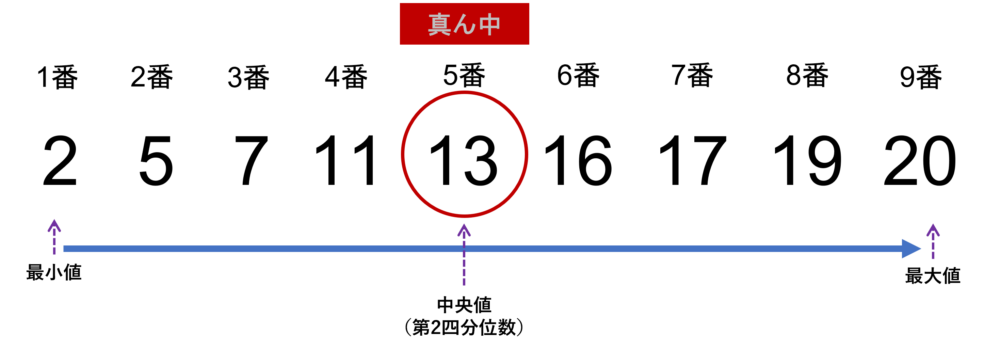
今回はデータが9個と、奇数であったこともあり、順番として真ん中のものが何であるかはイメージし易かったと思います。
つまり、データの数が奇数の場合と偶数の場合で求め方が違うことに留意が必要です。それぞれの場合の算出方法を示しますと
データの個数を n 、そしてkを正の整数、x(k)は、データを並べた際のk番目のデータと置きます。
- 【偶数の場合】 n= 2k , 中央値 =( x(k) +x(k+1)) /2
- 【奇数の場合】 n= 2k+1, 中央値 = x(k+1)
上記のように定義されます。
ここまでの例で示した9人のテストデータについては、上記の2の【奇数の場合】にあてはまり、つまり、k=4であることがわかりますね。そうすると、中央値はx(4+1)となり、5番目のx、つまり13であることがわかります。
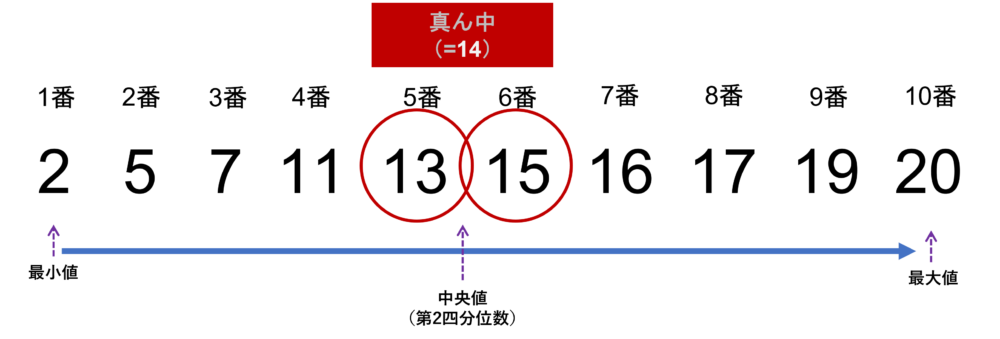
【偶数の場合】は、下記のイメージも参考ください。例えば、データの個数が10個であれば、k=5です。そして、中央値は x(5) と x(5+1) の2個のデータ(5番目と6番目のデータ)を足して2で割ればいいのです。それは13と15であり、その和は 28。 28を2で割り=14。これが中央値です。
第1四分位数、第3四分位数を求める(ステップ3)
続いてデータを、下位データと上位データに分けます。
実はここで、下位、上位のデータの分け方にも複数の定義があるのですが、その分け方の違いについては、後編のExcel作成編で説明します。今回は、下記の絵のように、中央の値を含まずに、第1(第3)四分位数を求めるやり方を説明します。(「排他的な中央値」を選定した場合と考えてください。)

下位、上位のかたまりにそれぞれ着目します。ここで再び、 下位(上位)データの数が奇数の場合と偶数の場合で求め方が違うことに留意が必要です。それぞれの場合の算出方法も中央値の算出と同様で、 下位(上位)データの個数を n 、そしてkを正の整数、x(k)は、データを並べた際のk番目のデータと置きます。
- 選択肢1【下位(上位)のデータ個数が偶数の場合】 n= 2k , 第1(第3)四分位数 =( x(k) +x(k+1)) /2
- 選択肢2 【下位(上位)のデータ個数が奇数の場合】 n= 2k+1, 第1(第3)四分位数 = x(k+1)
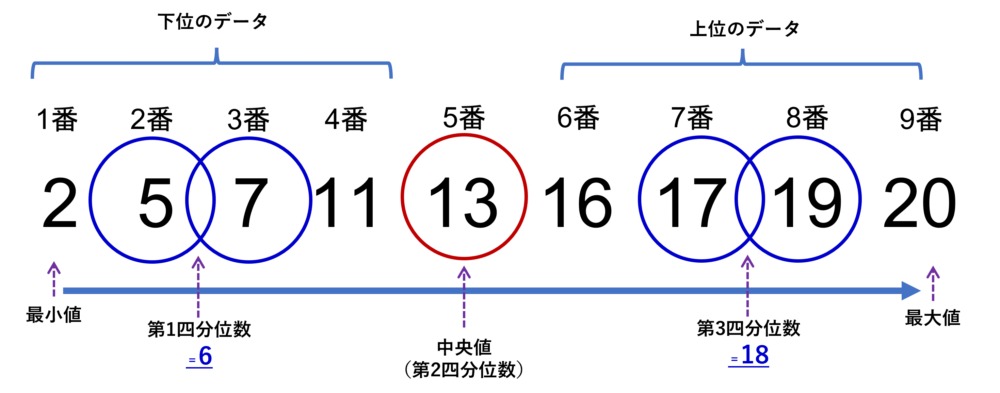
下位の方は個数が偶数で4つです。つまり、k=2ですね。そうすると、 第1四分位数は x(2) と x(2+1) の2個のデータ(2番目と3番目のデータ)を足して2で割ればいいのです。それは=6。 6が第1四分位数(lower quartile)そして、同様な考え方で、第3四分位数(upper quartile)は18であることがわかります。
また、下位(上位)データの個数が奇数であれば、選択肢2を選んで求めればいいだけですね。
これで四分位数が求まりました。
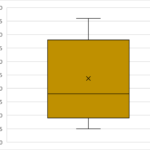
箱部分を四分位範囲と呼ぶ(第1四分位数~第3四分位数)
- 最小値
- 第1四分位数
- 中央値(第2四分位数)
- 第3四分位数
- 最大値
この5点をまとめて、五数要約(five-number summary)といいます。
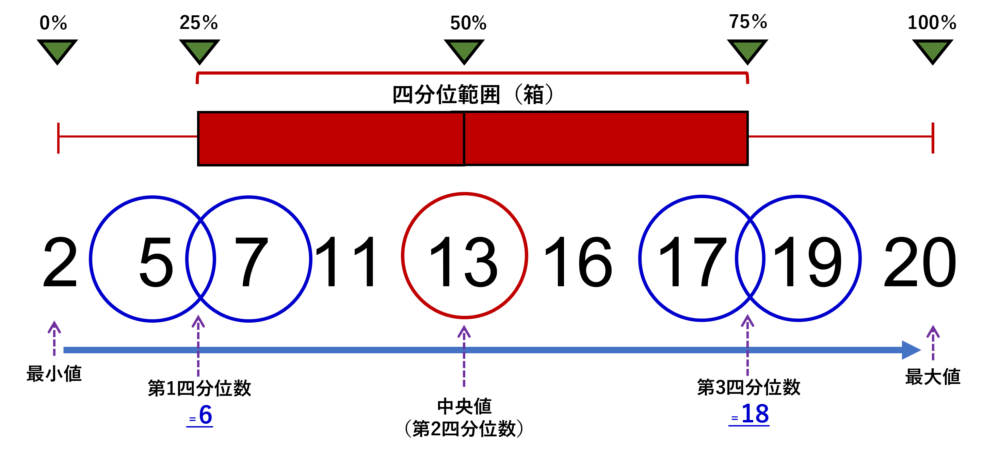
あらためて絵で示すと、左から0%, 25%, 50%, 75%, 100%としたものがそれぞれ上記の五数で、この25%地点の値が第1四分位数、50%の値が第2四分位数(中央値)であり、75%の値が第3四分位数となります。第1四分位数から第3四分位数までの範囲を四分位範囲(IQR)と呼び、絵のように箱で表します。また、箱に垂直に線を入れることで、中央値(第2四分位数)を示します。最小値~第1四分位数、第3四分位数~最大値は線(ひげ)で表すことで完成です。
IQRとは
IQRはInterquartile rangeからきている言葉で四分位範囲を表します。視覚化してみれば、まさに「箱」になりますね。
箱ひげの形から言えること
箱ひげ図では、ヒストグラムに代わり、データの分布をかたまりで視覚化してます。そして箱の部分が25%~75%で集まっている(中央の50%部)ことにより、この部分に着目させた図であると言えます。
箱ひげが全体的に長い(最小と最大の幅(差)が大きい)と視覚的に目立ちますが、データが分散的な感じがあります。逆に言えば、箱ひげの幅が小さいと、ばらつきが小さいとも言えます。その分、視覚的には目立ちません。特に、25%~75%の箱の部分の幅が大きいか、小さいかでデータがばらついているか、ばらついていないかが、ざっくりですが視覚的にわかります。
また、例ではデータ数(n数)は9個でしたが、箱ひげ図を使う場合、数値の羅列ではイメージしにくいものを、データ分布について視覚的にイメージし易くすることから、n数はより多い方が、使い勝手が良いでしょう。
外れ値について
もう1つ。外れ値について定義します。
データの中で値が突出していた場合は、「外れ値(Outlier)」として扱います。箱ひげ図では大きすぎても、小さすぎてもその場合、最大値・最小値はとはみなしません。ですので、箱ひげ図の外に表します。一般的には、以下のようになります。
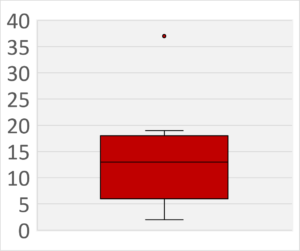
これは、Excelで表した、9人のテスト点数が下記のようになった場合の箱ひげ図となります。
2点、5点、7点、11点、13点、16点、17点、19点、37点
つまり、37点の方が、外れ値であることがわかります。
定義として外れ値は、
75%値(25%値) +(ー)1.5 × IQR
と、ここで求まる値より外側の値となると、箱ひげ部から外すように定義さております。もう少し丁寧に示せば、
- 「第3四分位数+1.5×四分位範囲」を超える値
- 「第1四分位数-1.5×四分位範囲」を超える値
が外れ値とみなされる値です。極端にいえば、Excel上では、上記9人目が36点では箱ひげの範囲に入りますが(※その場合、36点が最大値になります。)、37点となると、外れ値になります(「○○以上」ではなく、「超える値」であることに注意下さい)。
平均値について
ちなみに平均値についても説明します。平均値は箱ひげ図の統計的な観点から、強調するパラメータではないもと言えます。
箱ひげ図が、中央値を用いることで、実質的なデータの真ん中(中央の50%部)を表現するものに対し、平均値は確かに、全データの平均を取ること、「真ん中」を算出する手法ですが、集団から突出している数値が存在するとその数値に引っ張られてしまうという欠点があります。
とはいえ、Excel上ではグラフに示すことが可能であり、下記のようになります。”×”となったプロットが平均点です。
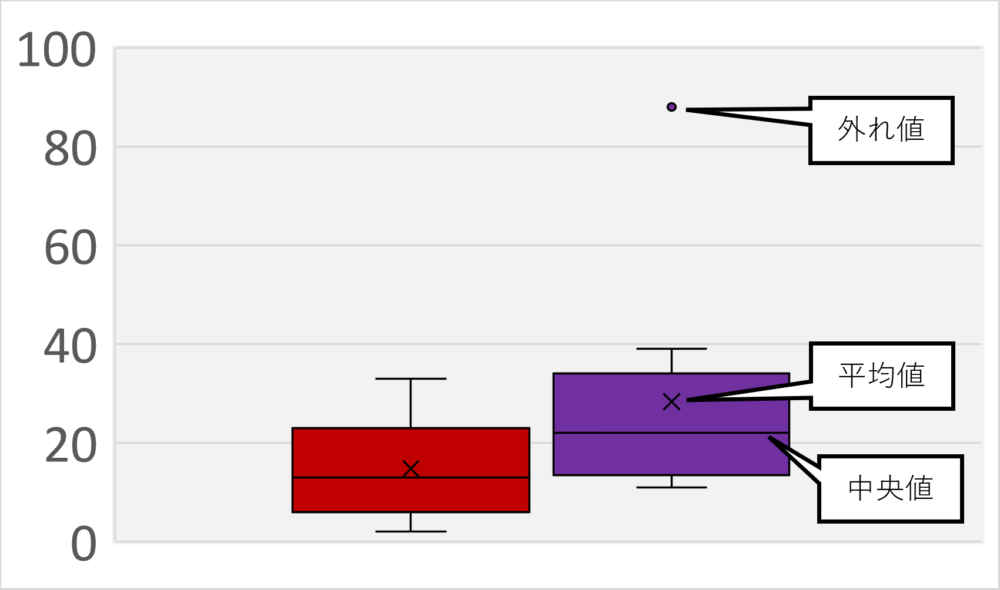
これをみると、右側の紫色の箱ひげ図が特徴的ですが、中央値と平均値の乖離が大きいですね。平均値が外れ値を含めた全データの総和を平均して得た値であるのに対し、中央値がデータを大きさ順に並べた際の真ん中にくる値であるから、この乖離が生まれるのがわかります。
ですので、平均値はExcel上で示すことは可能ですが、あくまで参考程度にみるべき指標と言ってよいでしょう。
箱ひげ図のメリット
では、この箱ひげ図を作るメリットは何でしょうか?
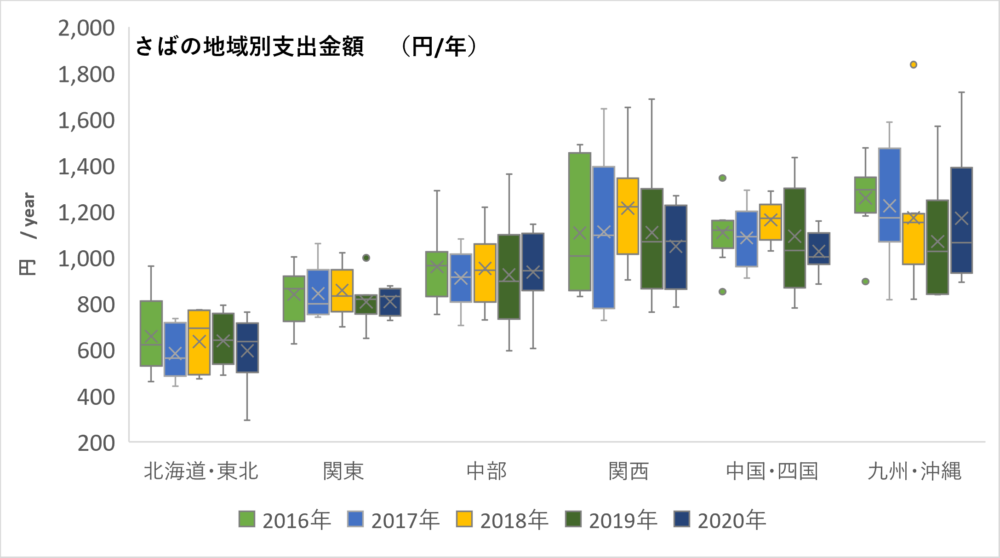
ちゃこぱの投稿では、多くの箱ひげ図を作成・掲載してます。今回の投稿でも冒頭で鯖の日本の地域別で1年間の支出額を2016年から、5年間、毎年みてました。
この1枚のグラフだけで多くの情報がありますね。
- 鯖の支出に対する毎年の傾向把握
- 地域別での比較
- ばらつき度合い(中央の位置)の把握
- 最大値、最小値を含めた五数要約の把握
が良くわかるのです。
多くの情報を1枚のグラフに濃縮
データのばらつき具合を把握する際によく使われるヒストグラムを念頭に置いて比較すると、極端に言えば、2016年の北海道・東北の分布でグラフ1枚・・、2017年の北海道・東北の分布でグラフ1枚・・・・
とすると、この鯖の支出額の情報をヒストグラムで表現するために各地域×5年間で合計30枚のグラフが必要です。
さすがに30枚なんて作る方も、確認する方も、一筋縄では行きませんよね。また、ヒストグラムでは五数要約は瞬時にはわからず、箱ひげ図でははっきりわかるのもメリットです。
箱ひげ図の最大のメリットとして、多くの重要な情報が1枚のグラフで全て一瞬でわかる、というものです。特にばらつき度合いを他と比較しながらレビューする、というのには最適と言っていいでしょう。
箱ひげ図のデメリット
データ分布の密集度合い、偏りがわからない
最大のデメリットが単一のデータのかたまりにおけるばらつき度合いを詳細には掴みにくいことが挙げられます。
例えば、狙いが25 gになるように設計する製品につき、実際に製造した33個のロットの重量の実測結果が以下だったとします。

上記から、25グラム狙いなのに、大小にわりとばらついているな、という印象を持ち、箱ひげ図で書いてみると、
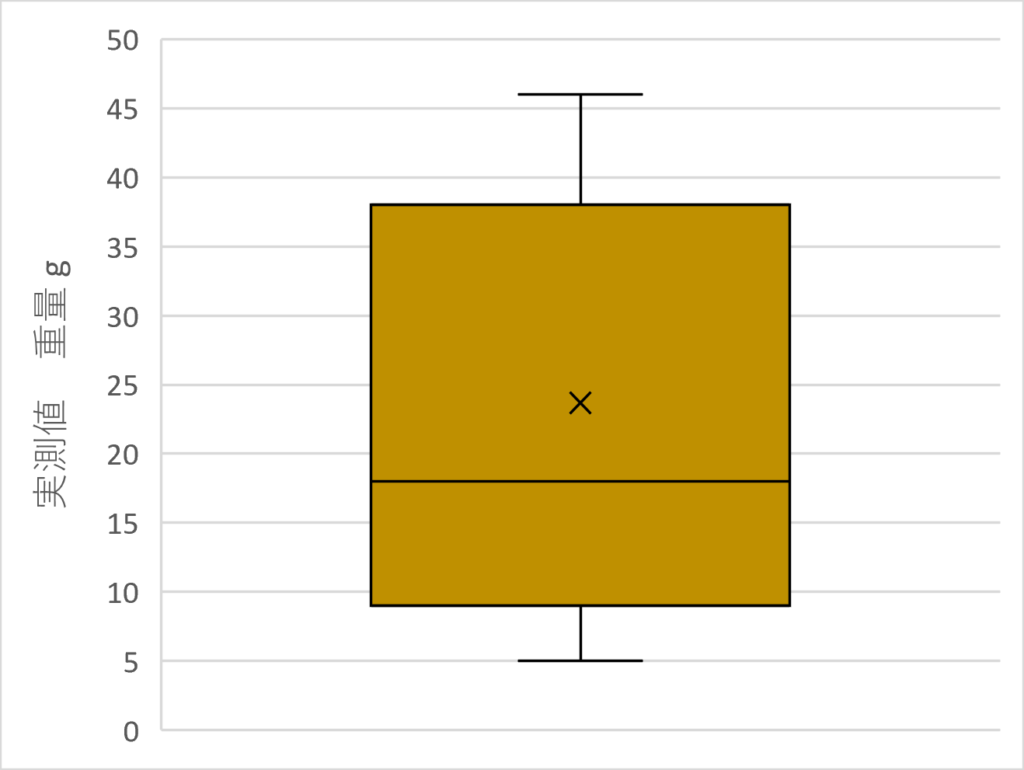
箱の部分(25~75%部)が長いな、と感じますね。ひげ部も含め大きい側も小さい側も25 gにできる限りなるよう、幅を狭めよう、というだけの話になるかと思います。
一方で、ヒストグラムでは33個のその実測値をグラフで示すと、
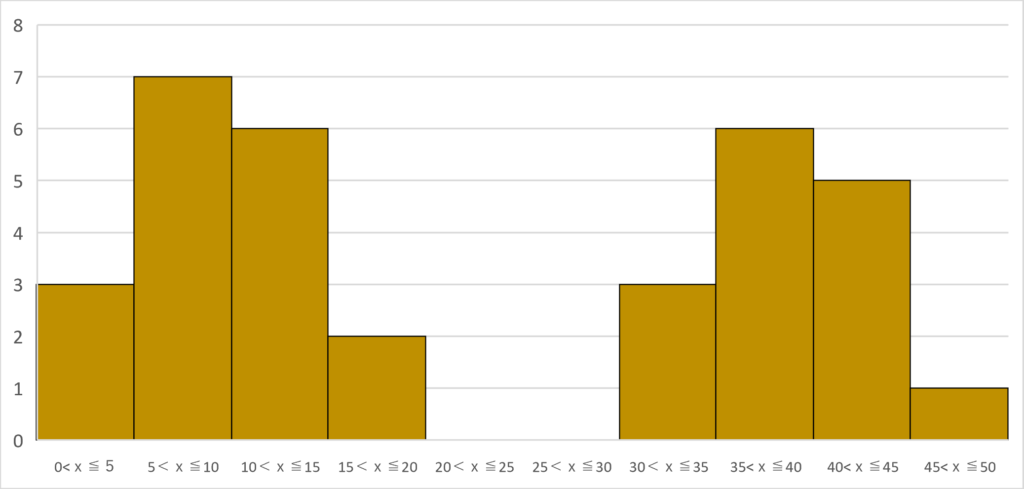
上記の通りで、なんとデータが2極化(山が2つある)していることがわかります。これは製造現場の原因・対策を打つような場面では、次の1手を決定するのに、ツールの使い方が重要にもなる典型例ですが、
例えばこの製品を造る途中工程で、Aという事象がおきてしまうと、25グラムより小さい側に製造してしまうかもしれず、一方で、途中でBという事象が発生すると、25グラムより大きい側に製造してまう、という何らかの仮説が、このヒストグラムによって立てることができるようになります。Aを回避するための対策、及びBを回避するための対策の検討が、それぞれ分けてできることになります。
このような仮説は、箱ひげ図だけでは難しいですね。
以上の例で示したように、この節の頭で言及した通り、 単一のデータのかたまりにおけるばらつき度合いを掴みにくく、次の一手を打つには、箱ひげ図では難しいといった、デメリットがあります。
目的に応じて、箱ひげ図とヒストグラムを使い分けることを念頭に置いていただければと思います。
John Tukeyについて
箱ひげ図の誕生はそれほど昔ではなく、1970年にアメリカの数学者、統計学者ジョン・チューキー(John Tukey)氏によって最初に紹介され、1977年に彼の著書で公開されたと言われております。社会への貢献度はいろいろな面であったことが調べるとわかります。
その中の1つとして、NBCというテレビでの選挙の予測や分析に使用する世論調査の設計に携わっていたようです。詳細はわかりませんが、数学者、統計学者が米国の政治にも関わっていたことは意外というか、印象的です。
後編にて公開
まとめに入る前に、箱ひげ図については、Excelの作成の仕方やその時の見方の説明を後編として投稿します。
ここで、ややこしくなりますが、Excelでは、第1四分位数と第3四分位数の決定の仕方が【排他的な中央値】か【包括的な中央値】を選択するかで、変わります。
Excelを使った作成についての説明は後編で細かく行いますので、後編をご一読ください。後編の投稿は下記となります。
まとめ
箱ひげ図とは何か?というテーマで説明をしてきました。
見方として、絵で示すと下記の通りでまとめます。見方のサマリーですね。
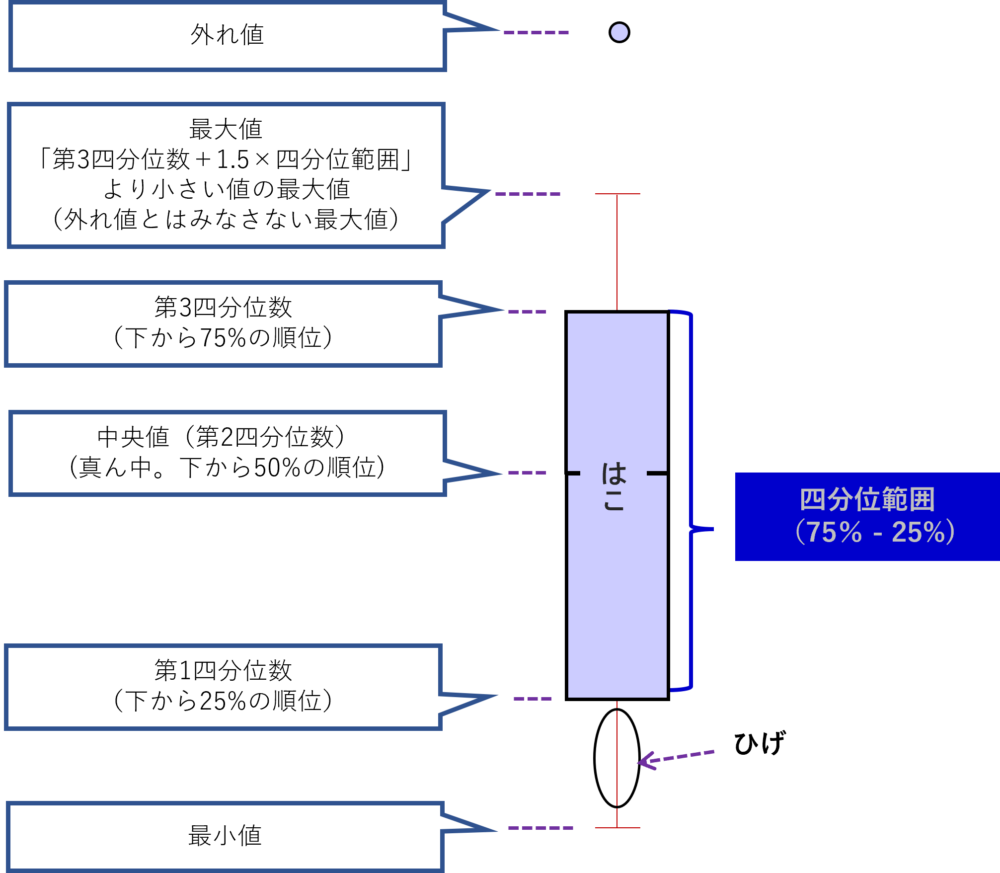
メリット:多くの重要な情報が1枚のグラフで一瞬でわかる、という点で優れた統計図
デメリット: 単一のデータのかたまりにおける、ばらつき度合いを掴みにくい
ということで、用途による使い分けを推奨します。ちゃこぱのブログでは、今後も箱ひげ図を大量に作り続けますけどね。
後編もよろしくお願いします。また通常投稿のオープンデータの料理も見ていただければ幸いです。
以上です。
ではでは@ちゃこぱ