はじめに
前編では、箱ひげ図そのものは何か、といった観点で見方や、関連する用語の説明、メリット・デメリットを説明しました。
では実際に箱ひげ図を作ってみましょう、ということでExcelを使って箱ひげ図を作ってみます。
Excelでの箱ひげ図の作り方

箱ひげ図を作る機能はExcel2016から搭載されたようで、簡単に作成が可能となっています。過去の情報(Excel2013以前)では、作成方法も古いため、今から学ぶ方は、簡単な方法であるExcel2016以降のやり方が楽でもありますので、参考にしてください。
Excel画面にて手順説明
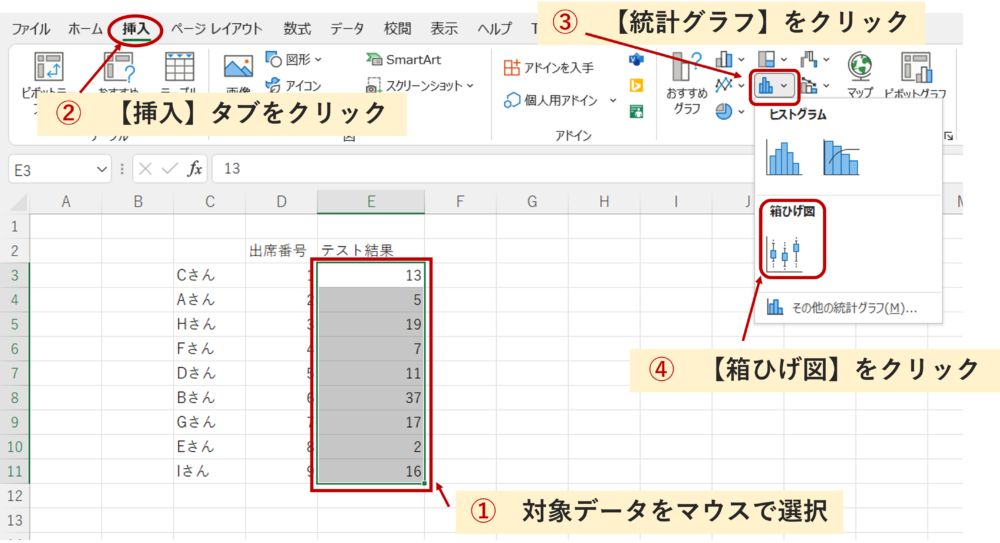
まずは、なんでもいいので、さっと箱ひげ図を作ってみたい、という方は早速Excelを開いて、複数個(例では9個)の数字を入力してみましょう。
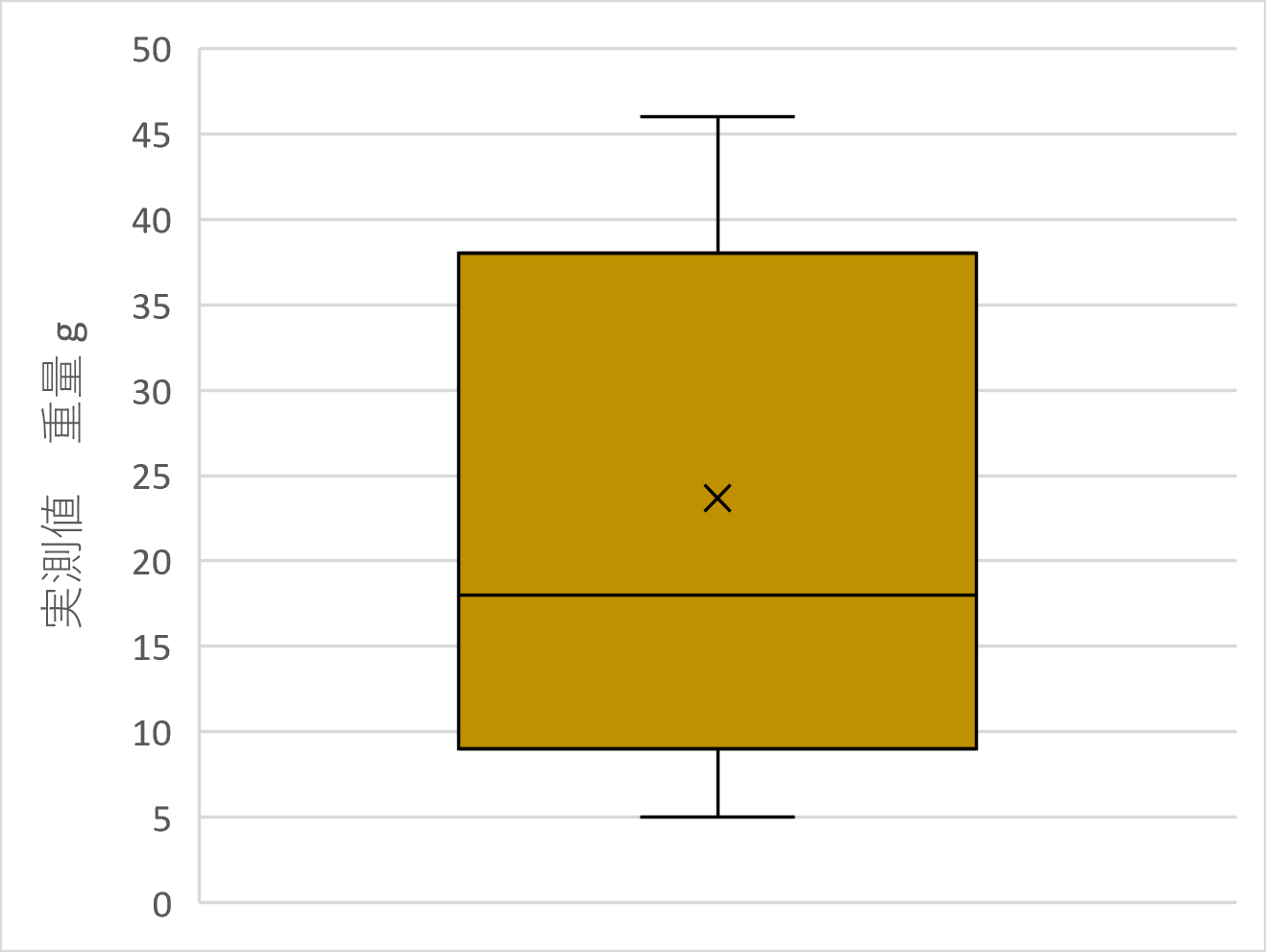
ここではAさん~Iさんの9名のテスト結果を箱ひげ図にしてみます。
①対象データを選択します。マウスを使って単に対象範囲のデータを選択した状態とします。②【挿入】タブをクリックします。③(複数のやり方がありますが、ここでは)【統計グラフ】をクリック④【箱ひげ図】をクリック。下記の通りです。
すると、簡単にデフォルトの箱ひげ図がExcel上に現れます。
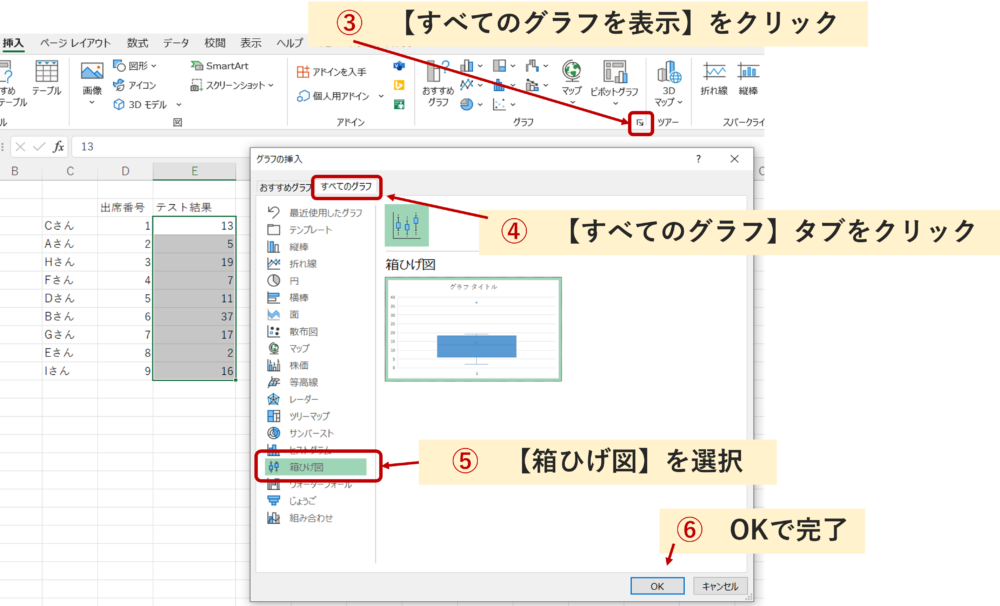
別のやり方もあります。上記①・②は同様で、その後③グラフタブの右下の【すべてのグラフを表示】をクリック、④【すべてのグラフ】タブを選択、⑤【箱ひげ図】を選択、⑥OKをクリックして完了です。
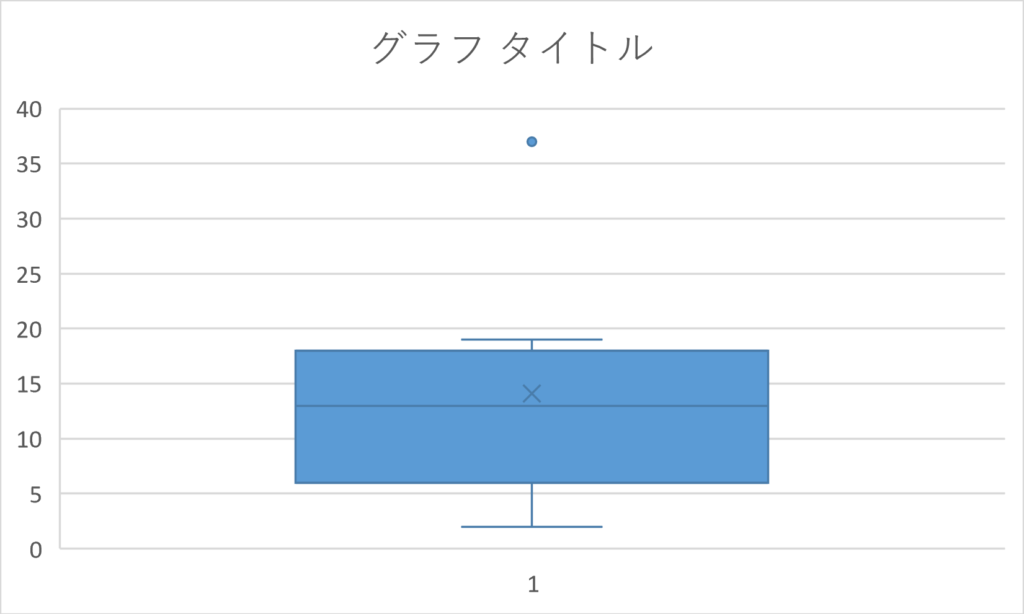
デフォルトの箱ひげ図は下記の通りです。
見せ方の追加・修正(データ系列の書式設定)
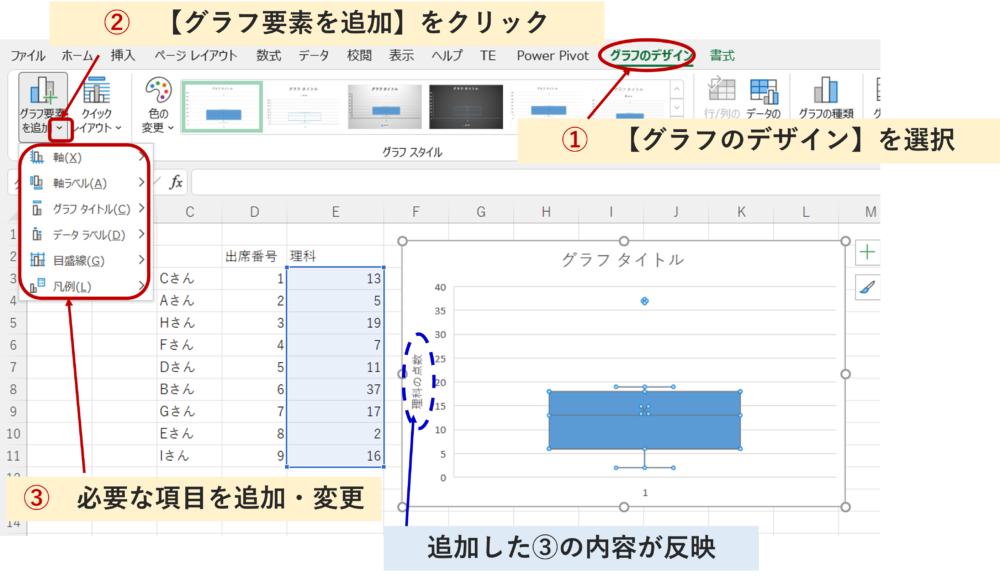
グラフの見せ方を追加・修正したい場合は、下記の絵を参考にしてください。例えばX軸名、Y軸名、凡例、グラフタイトルを加えることは頻繁に対応しますので、有用かと思います。
データ系列の書式設定
さて、グラフ上の箱ひげ図そのものを右クリックし、系列のオプションのタブを選ぶと、下記の絵が出てきます。
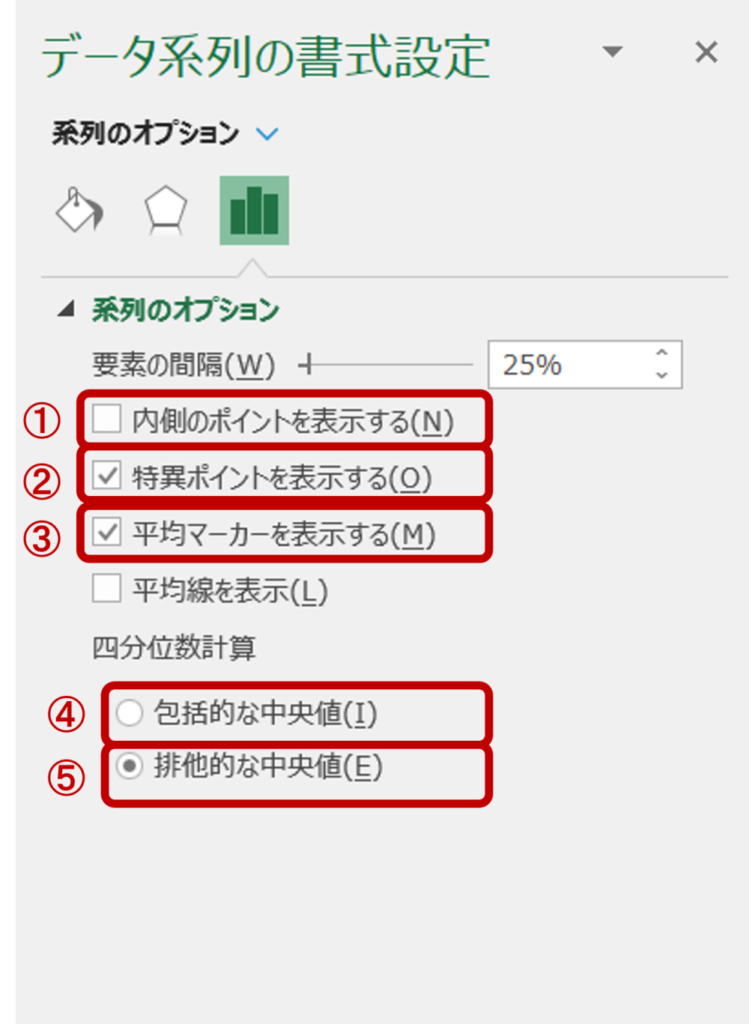
特筆すべき点として①~⑤まで挙げました。それぞれ申しますと、
① 内側のポイントを表示する
簡単に言えば、データそのものがプロットされてグラフに表示される(内側ポイントあり:チェック)か、複数のデータのプロットはなく、グラフが表示されるか(チェックなし)で違いが出ます。
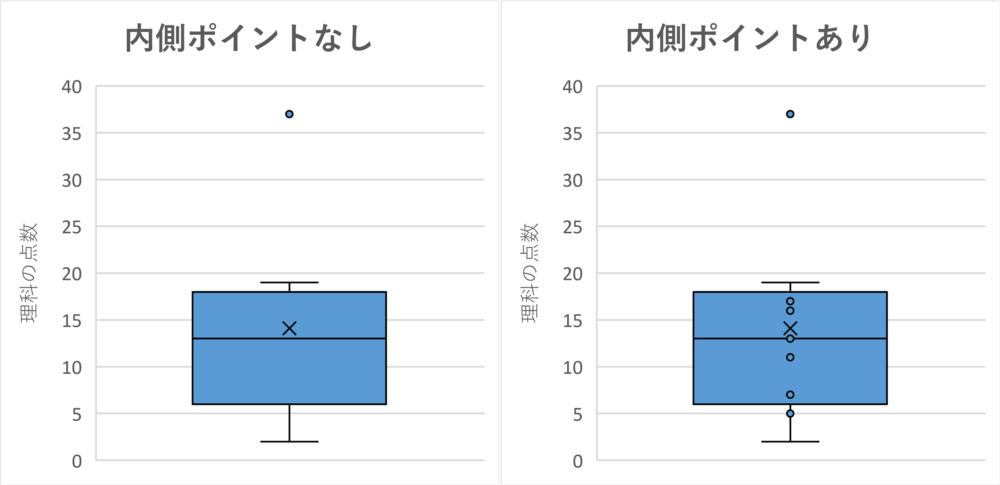
全体感を見せる程度であるなら、私の場合「内側ポイントなし」を適用することが多いです。
② 特異ポイントを表示する
特異ポイントとは、つまり外れ値のことです。その外れ値を考慮して箱ひげ図を作成するか、考慮せずに箱ひげ図を作るか、ということです。この投稿ページの全ての箱ひげ図について、外れ値を考慮していることがわかりますね。(上側に1プロット(37点というデータ)があり、箱ひげ図として形成されていない。)
基本的には、外れ値を考慮して、箱ひげ図を作成した方が良質な箱ひげ図になると考えます。つまり、「特異ポイントを表示する」にチェックを入れる方がベターです。勿論ケースバイケースでしょうが、外れ値を考慮しないと、外れ値が最大値(または最小値)となり、結果的に「はこ」部も「ひげ」部もこの値に引きずられてしまいます。状況によっては、歪な図となり、(外れ値をケアせず見ることとなり、)その後のレビュー・判断にも影響する可能性があります。
外れ値はOutlierと英語では言います。外れ値の定義、詳しい見方は前編の投稿で説明していますので、下記の投稿も参考にしてください。
③ 平均マーカーを表示する
平均値を箱ひげ図に入れるか、入れないか、ということです。”×印”で表します。箱ひげ図では中央値は必ず入ります。第二四分位数とも言いますが、それがあるがゆえに、箱ひげ図ができるものと言っていいでしょう。これも外れ値の見方と同様に、詳細な説明を前編の投稿でしていますので、参考にして下さい。
また、平均値を図に入れるべきか、入れないべきか?という観点では、これはどちらが多数派であるでしょうか?
なんとも言えない、半々なイメージを私は持っています。箱ひげ図のそもそもの成り立ちを考えれば、平均値の表示は不要かもしれません。しかし、中央値と平均値の乖離をみたい場合は、有用とも言えます。結局ケースバイケースで対応すればいいでしょう。
④と⑤の包括的な中央値と排他的な中央値は別の節にして、説明していきます。
包括的な中央値、排他的な中央値
投稿の前編ではこの2つの中央値の説明はしていませんでした。やや複雑な考えが入ってきますが、まずは概念的なイメージだけを解説していきます。この2つのどちらかを選択するかによって、四分位数が変わることを意味します。
包括的な中央値:中央値を含める(=包括する)
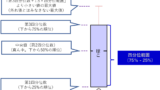
包括的な中央値は、中央値を含めて四分位数を計算することになります。概念的に絵で示しますと、
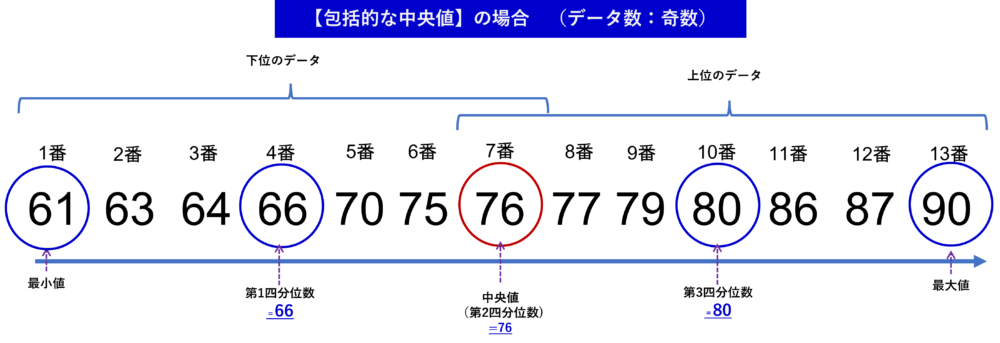
上記の通りです。下位のデータも、上位のデータのいずれも、真ん中の7番のデータを考慮しているのがわかりますね。データ13個のうち、左から小さい順に並べ、真ん中となる7番目の「76」が中央値(=第2四分位数)です。次に第1四分位数を求める場合、その中央値を含めて第1四分位数を求め、1番目~7番目の真ん中となる4番目の「66」が第1四分位数となります。
同様に中央値となる7番目を含めて、7~13番目の真ん中となる10番目の「80」が第3四分位数となります。
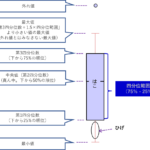
排他的な中央値:中央値を含まない(=排他する)
排他的な中央値は、中央値を含めずに四分位数を計算することになります。四分位数を計算するにあたり、どちらを選定するかで、四分位数が変わることを意味します。概念的には、下記の通りです。
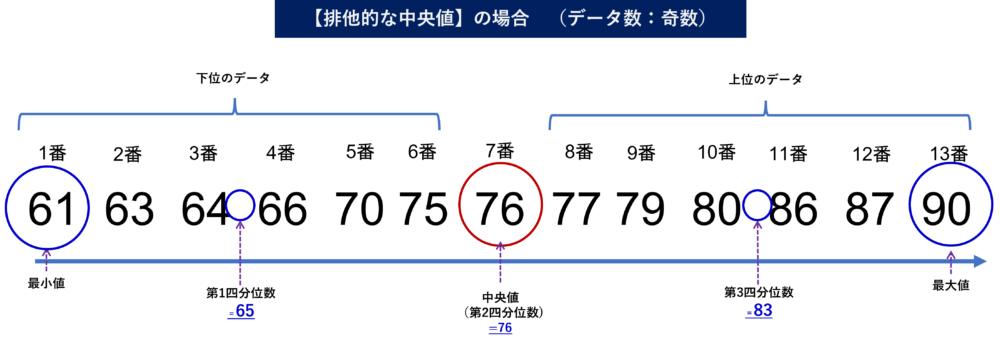
中央値自体の求め方は、包括的な場合の求め方と変わりませんが、第1四分位数、第3四分位数を求める場合に、いずれもこの中央値を含めずに(=排他して)求めることとなります。この絵では7番が下位・上位のデータにも選択されていないことがわかります。
それぞれ、そのデータ数の中の真ん中のものが、各四分位数となりますが今回、いずれも6個(1~6番、8~13番)で偶数となるため、その場合、前編の投稿でも示した、やり方として、
偶数として、データがそれぞれ6つです。つまり、k=3ですね。そうすると、 第1四分位数は x(3) と
x(3+1) の2個のデータ(下位のデータの場合:3番目と4番目のデータ)を足して2で割ればいいのです。それは=65。 65が第1四分位数、そして、同様な考え方で、第3四分位数は83であることがわかります。
Excelでグラフ化して比較すると・・
実際にExcelで箱ひげ図を作って比較してみましょう。
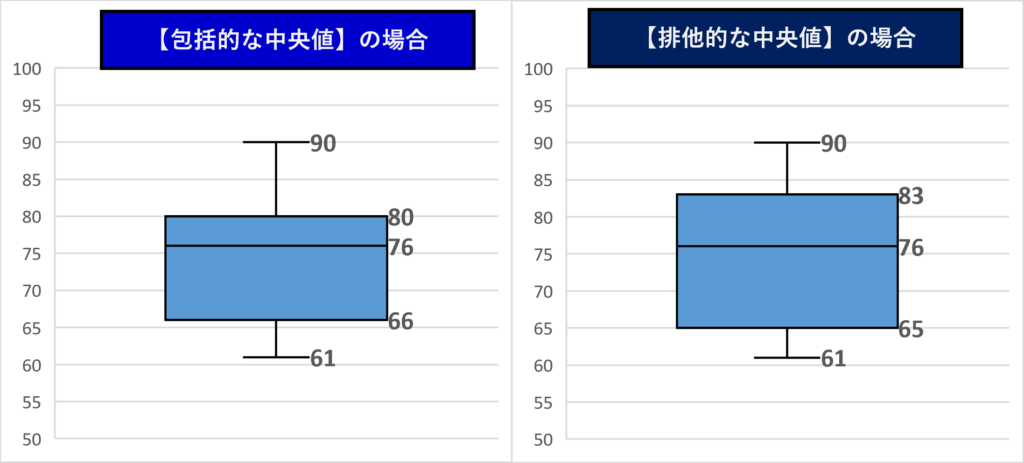
Excelの設定にて、箱ひげ図自体を右クリックして、【データラベルの追加】を選定することで、グラフ上に五数要約(最大値、最小値、第1四分位数、中央値、第3四分位数)を表示させることができます。
グラフを見てもわかる通り、右の排他的な中央値の場合は、第1, 第3四分位数が【包括的な中央値】の場合と違いますね。ひげ部が短く、言い換えれば、箱部が長いですね。つまり、包括的な中央値、排他的な中央値のどちらを選ぶかによって、箱部・ひげ部の長さが違う(第1, 第3四分位数が変わる)ことがわかります。
ちなみに、データ数が多い場合には、この箱部、ひげ部の違いが出にくくなる傾向があります。今回はデータ数が13個のみでした。この程度であれば違いが分かりやすく出ますが、箱ひげ図の本質的には、大量のデータを、複数の括りで比較しながら、ばらつき度合い・データ分布を容易にレビューすることに優れたツールですから、あまり、包括的・排他的な中央値の設定にこだわる必要もないと考えます。勿論、場合にも依りますが、次の節でさらにこだわる場合の話もします。(おまけの話になります。)
データ数が偶数の場合:おまけ編で説明
今回の例で示した例はデータ数が奇数の場合で説明をしました。実は、概念的なとらえ方としては奇数の場合の方がわかりやすく説明できたのが理由ですが、一方でデータ数が偶数の場合は、少し包括的・排他的な中央値について深堀りを加えながら、説明する方がベターです。
ただし、先述の通り、箱ひげ図の最大のメリットが、大量のデータを濃縮した1枚のグラフに料理することで、全てが一瞬でわかる、というものですので、データのn数が奇数か偶数か、というのは強く意識する必要はありません。したがって、偶数の場合の包括的・排他的な中央値をもとにした、第1, 第3四分位数を、細かく精査する話は、実務上、特段重要でもありませんので、次回の箱ひげ図の続きの解説はあくまで「おまけ編」として投稿する予定です。
複数のデータを1枚にまとめた例
ここまでの例では、1つのデータ群を箱ひげ図にしただけでしたが、最大のメリットと言い続けている、複数のデータをまとめて示す場合のやり方を説明します。
と言っても、複数のデータを表す場合でも大変簡単です。
例えば、魚の蛸(たこ)の支出額(円)といったデータがあるとします。しかも、地域別に毎年、この5年間のデータがあるとした場合、データ自体はいったん、以下のように、行に地域別、列で年別にまとめればOKです。(注:この例でもn数は少なめです。)
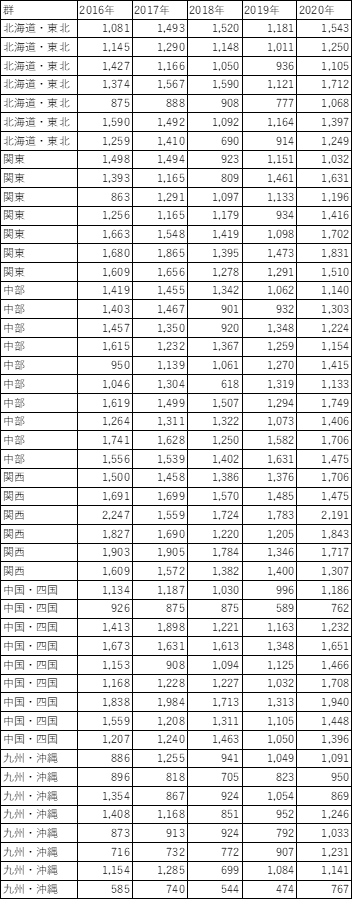
上記のようにExcelで表にしたら、この表そのものを、マウス等で選択した状態で、前半部で示した同一の手順で箱ひげ図にすればよいだけです。(自動的に、Excelが下の絵のように箱ひげ図化してくれます。)
その後は見やすさを変える為だけの書式系列の設定、色の塗りつぶし設定等を変えて、以下の通りとしています。
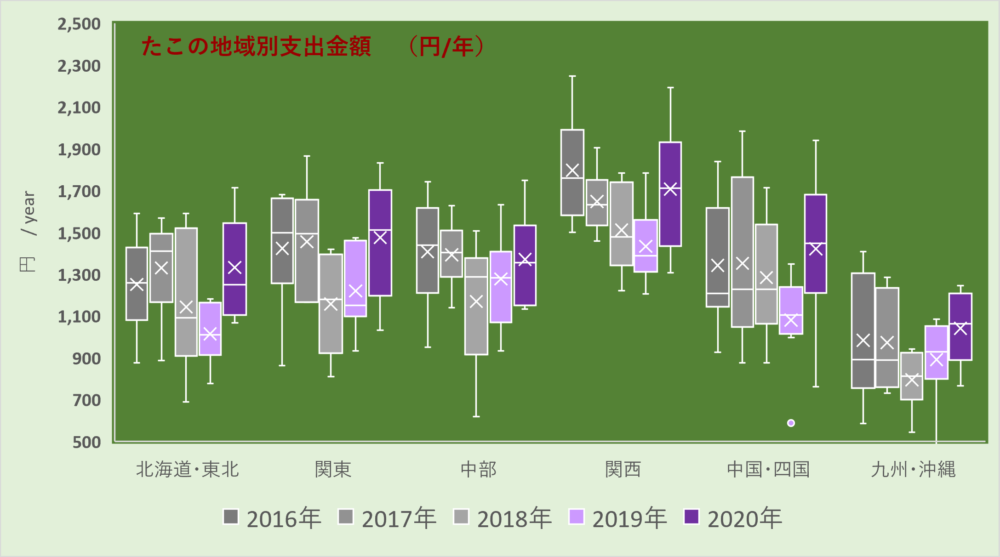
表だけでは何とも印象がわからない、その後の意思決定にもつながらないデータを、たった1枚の上記箱ひげ図を作ることによって、幾つか傾向が見えてきたりしますね。たこの支出額に関する傾向の深堀りはこれ以上はしませんが、これが箱ひげ図を作成するメリットでしょう。
まとめ
今回は主に3点、説明をしました。
- Excelでの箱ひげ図のグラフを作成にあったてのその手順
- データ系列の書式設定による箱ひげ図の表示上の追加・変更(①内側ポイント ②外れ値 ③平均値)
- 包括的な中央値、排他的な中央値の考え方
複数の群として、あるデータのまとめ方も例として挙げました。簡単に図として表すことでき、次のステップに進めやすくなることを実感いただけたかと思います。
前編・後編として解説しました箱ひげ図の定義の解説は以上です。後日、おまけ編として 包括的・排他的な中央値の深堀りをExcel関数を通じて、解説していきたいと思います。そちらもお楽しみに。
また通常投稿のオープンデータの料理も見ていただければ幸いです。新たな投稿も続けていきます。
以上です。
ではでは@ちゃこぱ